 es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien 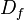 . En
. En  se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.
se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.
El dominio de definición de una función f:X→Y se define como el conjunto X de todos los elementos x para los cuales la función f asocia algún y perteneciente al conjunto Y de llegada, llamadocodominio. Esto, escrito de manera formal:
También se podría decir en términos más simples que son todos los posibles valores que tiene x en una función.
Ejemplos:
11.-
12.-
13.-
14.-
15.-
f(x)=√-x en este ejercicio debes observar que se trata de una raíz cuadrada es decir de índice
par por lo tanto su radicando debe ser mayor o igual a 0 por lo tanto como apareceel menos que precede a x sabemos que cambia su signo El dominio son todos los
números reales menores o iguales a 0
La imagen son los números reales mayores o iguales a 0
16.- g(x)= 1/x-2 en este caso es muy importante considerar que el denominador nunca debe ser 0
por lo tanto el Dominio está dado por todos los números reales menos {2}
La imagen o rango son todos los números reales menos {0}
17.- h(x)= 3/√x-4 Aquí debe considerarse por un lado que el denominador no puede ser 0 y además
por la raíz de índice par el radicando debe ser mayor o igual a 0
x - 4 > 0 luego x > 4 entonces el dominio es el conjunte los números reales
mayores que 4
La imagen son los números reales positivos
18.- 5(x)= x+2/√9-x Igual que en el caso anterior debe considerarse en el denominador que debe ser
distinto de 0 y por tratarse de una raíz de índice par el radicando debe ser mayor
que 0
9 - x > 0 x <9 El dominio son todos los números reales menores que 9
El rango son todos los números reales mayores que 0
19.-
Función f(x) = 1/x tiene su dominio en todos los números reales menos cuando x = 0 ya que 1/x no existe, es decir, (menos infinito, 0) U (0, mas infinito).
20.- Función: f(x) = log(x), el dominio de esta función es todo los valores reales desde el 0 (sin contar con el) hasta el infinito, es decir, (0, infinito).
Haz clic aquí y verás un tutorial de dominio de una función.






No hay comentarios:
Publicar un comentario