Gráficas de Polinomios de la forma x n
Comportamiento a largo plazo de una función polinómica
Considerar la siguiente tabla que contiene los valde| x | -1000 | -100 | -10 | -1 | 0 | 1 | 10 | 1000 | 1000 |
|---|---|---|---|---|---|---|---|---|---|
| f(x) | 1000000 | 10000 | 100 | 1 | 0 | 1 | 100 | 10000 | 1000000 |
| g(x) | 996005 | 9605 | 65 | 2 | 5 | 10 | 145 | 10405 | 1004005 |
| x | -1000 | -100 | -10 | -1 | 0 | 1 | 10 | 1000 | 1000 |
|---|---|---|---|---|---|---|---|---|---|
| f(x) | -2.000×109 | -2.000×106 | -2000 | -2 | 0 | 2 | 2000 | 2.000×106 | 2.000×109 |
| g(x) | -2.002×109 | -2.020×106 | -2224 | -1 | 6 | 9 | 1836 | 1.980×106 | 1.998×109 |
Conclusión: Cuando la magnitud de x es grande los valores de g(x)=axn +... se parecen a los valores de f(x)=axn.
La aplicacion de abajo, muestra las gráficas de g(x)=axn y f(x)=axn + ...
Cambia el zoom para verificar que las gráficas se ven iguales cuando los valores de x cubren un rango amplio. También puedes presionar el boton de la parte superior derecha para conseguir otra función f:
Recuerda que r es una raíz simple de f(x), si el factor (x-r) aparece una sola vez en la fórmula factorizada de f(x).
En la aplicación de arriba debemos poder observar que la gráfica cerca a una raiz simple se ve como:
En la aplicación de arriba debemos poder observar que la gráfica cerca a una raiz doble se ve como:
En la aplicación de arriba debemos poder observar que la gráfica cerca a una raiz triple se ve como:
| Si una función polinomial tiene una raíz r de multiplicidad k, entonces: La gráfica de la función cruza el eje x si k es impar. La gráfica de la función toca el eje x pero no lo cruza, si k es par. |
Las raíces de la función polinomial
x=-3 (multiplicidad 2), x=-2 (multiplicidad 1), x=0 (multiplicidad 3) y x=3 (multiplicidad 4).
La gráfica de esta función es la siguiente:
Haga clic en el siguiente enlace para practicar los conceptos gráficos relacionados a las raíces de un polinomio:
Cambio de signos de una función polinómica
Una función polinómica es continua, por lo tanto, su gráfica no se corta en ningún punto. Por esta razón las funciones polinómicas solo cambian de signo en sus raíces. Gráficamente esto significa que, entre dos raíces consecutivas, la gráfica esta completamente por encima del eje x o completamente por debajo del ejex. En la lección de Inecuaciones Polinómicas y Racionales utilizamos este hecho para evaluar el signo de un polinomio en un intervalo de prueba.Ejemplo:
Considera la función polinómica:
Factorizamos para obtener sus raíces:
Intervalo
|
Punto de Prueba
|
Función evaluada en el punto de prueba
|
Signo del Intervalo
|
| | x = -4 | | |
| | x = -1 | | |
| | x = 0.5 | | |
| | x = 2 | |
Graficar una función polinómica
Ya tenemos las herramientas para graficar polinomios. Los pasos para hacerlos son los siguientes:- Graficar raíces reales. Factorizar si es necesario.
- Identificar el signo de cada región.
- Hallar el intercepto en y.
- Trazar la gráfica pasando por las raíces y el intercepto. El trazo debe ser consistente con los signos y el comportamiento a largo plazo.
Ejemplo 1:
Graficar la función
Solución:
| Paso 1: Graficar raíces reales. Factorizar si es necesario. Factorizando la expresión obtenemos:
Las raíces definen los siguientes intervalos donde la función tiene el mismo signo. | ||||||||||||||||||||
Paso 2: Identificar el signo de cada región.
| ||||||||||||||||||||
| Paso 3: Hallar el intercepto en y. El intercepto en y es el valor de la función donde x=0, es decir, f(0). | ||||||||||||||||||||
Paso 4: Trazar la gráfica pasando por las raíces y el intercepto. El trazo debe ser consistente con los signos y el comportamiento a largo plazo.
| ||||||||||||||||||||
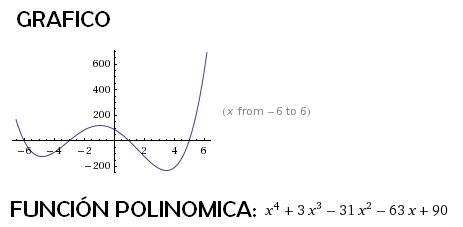
Ejemplo 2:
Graficar la función
Solución:
| Paso 1: Graficar raíces reales. Factorizar si es necesario. La expresión ya está factorizada:
Las raíces definen los siguientes intervalos donde la función tiene el mismo signo. | ||||||||||||||||
Paso 2: Identificar el signo de cada región.
| ||||||||||||||||
| Paso 3: Hallar el intercepto en y. El intercepto en y es el valor de la función donde x=0, es decir, f(0). | ||||||||||||||||
Paso 4: Trazar la gráfica pasando por las raíces y el intercepto. El trazo debe ser consistente con los signos y el comportamiento a largo plazo.
| ||||||||||||||||