Funciones polinomiales de tercer grado.
Una ecuación de tercer grado o ecuación cúbica con una incógnita es una ecuación que se puede poner bajo la forma canónica:
 ,
,
donde a, b, c y d (a ≠ 0) son números que pertenecen a un campo, usualmente el campo de los números reales o el de los números complejos.

La función cúbica es una función polinómica de tercer grado. Tiene la forma:
donde el coeficiente a es distinto de 0.
Tanto el dominio de definición como el conjunto imagen de estas funciones pertenecen a los números reales.
La derivada de una función cúbica genera una función cuadrática y su integral una función cuártica.
Ecuación cúbica
Ecuación cúbica
La ecuación cúbica es la ecuación que resulta de igualar a cero la función cúbica, y tiene la forma canónica:
donde a, b, c y d (a ≠ 0) son números que pertenecen a un campo, usualmente el campo de los números reales o el de los números complejos.
Discriminante
Resulta importante y a la vez esencial obtener propiedades elementales de los polinomios como herramientas de análisis en los resultados según los valores de sus coeficientes. Cualquier ecuación cúbica (1) con coeficientes reales tiene al menos una solución x sobre los números reales; esta es una consecuencia del teorema del valor intermedio. Se pueden distinguir varios posibles casos, usando para ello el discriminante,
Los siguientes casos necesitan ser considerados: 1
- Si Δ > 0, entonces la ecuación tiene tres distintas raíces reales.
- Si Δ = 0, entonces la ecuación tiene múltiples raíces y todas sus raíces son reales (puede ser una raíz triple o una doble y otra simple).
- Si Δ < 0, Entonces la ecuación tiene una raíz real y dos raíces complejas conjugadas.

Las primeras ecuaciones de tercer grado que se intentó resolver fueron con coeficientes reales (de hecho: enteros). El cuerpo de los reales no es algebraicamente cerrado, por lo tanto, el número de raíces reales no es siempre 3. Las que faltan se encuentran en C, extensión algebraica cerrada de R. La distinción aparece cuando se calcula el discriminante de la ecuación. Se puede notar que siempre hay por lo menos una solución real, independientemente de que el discriminante Δ sea mayor, menor o igual a cero. Es debido a que las funciones polinomiales no constantes tienen límites infinitos en +∞ y -∞ y las de grado impar tienen límites de signos contrarios. Como son funciones continuas, tienen que pasar por cero, por el teorema de los valores intermedios.
También es posible resolverla con el método de Newton-Raphson, ya que se sabe que al menos habrá una solución real.
Raíces reales de la ecuación cúbica
Partiendo de la ecuación canónica
dividiendo entre a y haciendo una transformación de Tschirnhaus (sustituyendo  ) se elimina de la forma normal el término cuadrático y se obtiene la forma reducida:
) se elimina de la forma normal el término cuadrático y se obtiene la forma reducida:
 ) se elimina de la forma normal el término cuadrático y se obtiene la forma reducida:
) se elimina de la forma normal el término cuadrático y se obtiene la forma reducida:
con lo cual,
Se demuestra que el número de raíces reales depende del discriminante de la ecuación auxiliar  .2 La ecuación cúbica incompleta
.2 La ecuación cúbica incompleta  posee tres raíces reales cuando el discriminante
posee tres raíces reales cuando el discriminante 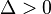 , pero donde
, pero donde  y
y 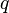 posee cualquier valor y signo. Tales raíces se calculan como
posee cualquier valor y signo. Tales raíces se calculan como
 .2 La ecuación cúbica incompleta
.2 La ecuación cúbica incompleta  posee tres raíces reales cuando el discriminante
posee tres raíces reales cuando el discriminante 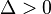 , pero donde
, pero donde  y
y 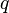 posee cualquier valor y signo. Tales raíces se calculan como
posee cualquier valor y signo. Tales raíces se calculan como , para
, para 
donde el signo positivo se usa si  y el signo negativo se usa si
y el signo negativo se usa si  . Mientras que
. Mientras que 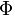 esta dada por
esta dada por
 y el signo negativo se usa si
y el signo negativo se usa si  . Mientras que
. Mientras que 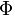 esta dada por
esta dada por
De modo que si queremos calcular las tres raíces de la ecuación cúbica completa  , entonces podemos obtenerlas fácilmente como
, entonces podemos obtenerlas fácilmente como
 , entonces podemos obtenerlas fácilmente como
, entonces podemos obtenerlas fácilmente como , para
, para 
- Ejemplo.
- Sea la ecuación cúbica
 , Se procederá a resolverla, para ello, se siguen los siguientes pasos.
, Se procederá a resolverla, para ello, se siguen los siguientes pasos. (al dividir por 2)
(al dividir por 2)- Con x = t + 1, es decir t = x - 1, reemplazando:
-
 , y desarrollando, se optiene la ecuación en forma reducida
, y desarrollando, se optiene la ecuación en forma reducida  .
.
- x = u + v, U = u³, V = v³ y se impone U + V = - 1 y UV = - 1. U y V son las raíces de X² + X - 1 = 0.
- Se despeja U, V y t.
-
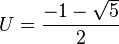 y
y  , luego
, luego ![u = \sqrt[3]{\frac {-1 - \sqrt {5}} {2}} \,](http://upload.wikimedia.org/math/0/2/8/028fb28ea5a3c116efa26ad70b76cfa7.png) y
y ![v = \sqrt[3]{\frac {-1 + \sqrt {5}} {2}} \,](http://upload.wikimedia.org/math/3/b/3/3b301c212acc6496fd958be984308ec0.png) .
.
- Por lo tanto
-
![t = x - 1 = u + v - 1 = \sqrt[3]{\frac {-1 - \sqrt {5}} {2}} + \sqrt[3]{\frac {-1 + \sqrt {5}} {2}} - 1 \approx -1,3221853546](http://upload.wikimedia.org/math/5/1/3/513472e74ff72db470860f9c127f9789.png)

 .
.- Dividir la ecuación inicial por el coeficiente a. Se obtiene:
 , donde
, donde  ,
,  ,
,  y
y 
- Proceder al cambio de incógnita
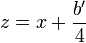 , para suprimir el término cúbico. En efecto, al desarrollar
, para suprimir el término cúbico. En efecto, al desarrollar  con la identidad precedente, vemos aparecer el término
con la identidad precedente, vemos aparecer el término 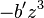 , compensado exactamente por
, compensado exactamente por  que aparece en
que aparece en  . Tras sustituir x y operando con las identidades notables, se obtiene:
. Tras sustituir x y operando con las identidades notables, se obtiene: 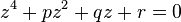 , con p, q y r números del cuerpo.
, con p, q y r números del cuerpo.- Y ahora, la idea genial: factorizar lo anterior en
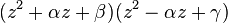 , lo que es posible porque no hay z³ en el polinomio.
, lo que es posible porque no hay z³ en el polinomio.  (coeficiente de x²)
(coeficiente de x²) (coeficiente en x)
(coeficiente en x) (término constante)
(término constante) , que resulta ser una ecuación de tercer grado en la variable
, que resulta ser una ecuación de tercer grado en la variable 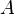 y que se puede resolver usando el método de Cardano.
y que se puede resolver usando el método de Cardano.


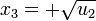

- Otro caso particular: Ecuaciones casi-simétricas
Funciones polinomiales de grado cuatro.
 Una ecuación de cuarto grado o ecuación cuártica con una incógnita es una ecuación que se puede poner bajo la forma canónica:donde a, b, c, d y e (siendo
Una ecuación de cuarto grado o ecuación cuártica con una incógnita es una ecuación que se puede poner bajo la forma canónica:donde a, b, c, d y e (siendo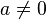 ) son números que pertenecen a un cuerpo, usualmente a los reales
) son números que pertenecen a un cuerpo, usualmente a los reales  o los complejos
o los complejos  .
.Caso general
Sea K un cuerpo, donde se pueden extraer raíces cuadradas y cúbicas (y por lo tanto también de cuarto orden, pues equivale a extraer raíces cuadradas dos veces seguidas). En este cuerpo, es posible factorizar por todo a, y la identidad siguiente es válida:En un cuerpo algebraicamente cerrado, se sabe que todo polinomio de grado 4 tiene cuatro raíces. Es el caso del cuerpo de los complejos, según el Teorema Fundamental del Álgebra.El método siguiente permite obtener las cuatro raíces al mismo tiempo. Este método es llamado "método de Descartes", pues fue dado por el matemático francés René Descartes (1596-1650) en el año de 1637 en su célebre libro "La Geometría". Aunque existan diferentes métodos para resolver las ecuaciones cuárticas, algunos son: método de Ferrari, método de Descartes, método de Euler, método de Lagrange, método de Alcalá, etcétera.
Método de DescarteLos pasos de la resolución para el método de Descartes (1637) son:Desarrollando la expresión e identificando los dos polinomios, obtenemos las condiciones:Después de algunos cálculos, hallamos : Es una ecuación de sexto grado, pero si miramos bien, α sólo aparece con potencias pares.Pongamos
Es una ecuación de sexto grado, pero si miramos bien, α sólo aparece con potencias pares.Pongamos . Entonces:Luego se encuentra α, β y γ, y se resuelven
. Entonces:Luego se encuentra α, β y γ, y se resuelven y
y 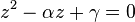 , y para terminar, no olvide que
, y para terminar, no olvide que  .Ecuaciones bicuadradaÉstas son un caso particular de las anteriores. Les faltan los términos a la tercera y a la primera potencia. Su forma polinómica es:Para resolver estas ecuaciones tan solo hay que hacer el cambio de variable
.Ecuaciones bicuadradaÉstas son un caso particular de las anteriores. Les faltan los términos a la tercera y a la primera potencia. Su forma polinómica es:Para resolver estas ecuaciones tan solo hay que hacer el cambio de variable
Con lo que nos queda: El resultado resulta ser una ecuación de segundo grado que podemos resolver usando la fórmula:
El resultado resulta ser una ecuación de segundo grado que podemos resolver usando la fórmula: Ahora bien, esto no nos da las cuatro soluciones esperadas. Aún hemos de deshacer el cambio de variable. Así las cuatro soluciones serán:El siguiente tipo de ecuación
Ahora bien, esto no nos da las cuatro soluciones esperadas. Aún hemos de deshacer el cambio de variable. Así las cuatro soluciones serán:El siguiente tipo de ecuación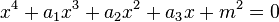 , donde
, donde  , puede ser resuelto así:Al dividir la ecuación por
, puede ser resuelto así:Al dividir la ecuación por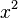 , se obtiene
, se obtiene
 Haciendo cambio de variable:
Haciendo cambio de variable: llegamos a
llegamos a
Así
Esta ecuación da 2 raíces, y
y 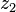 Las raíces de la ecuación original pueden ser obtenidas resolviendo las siguientes ecuaciones de 2o grado:
Las raíces de la ecuación original pueden ser obtenidas resolviendo las siguientes ecuaciones de 2o grado: y
y Si
Si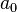 no es 1 en
no es 1 en  este método es de todas formas aplicable, luego de dividir la ecuación entre
este método es de todas formas aplicable, luego de dividir la ecuación entre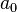 .Las ecuaciones cuasi simétricas poseen la siguiente propiedad, que, por otra parte, las define: si
.Las ecuaciones cuasi simétricas poseen la siguiente propiedad, que, por otra parte, las define: si ,
, 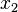 , y
, y  ,
, son las raíces de la ecuación, entonces
son las raíces de la ecuación, entonces  . Dado que el producto de las 4 raíces es
. Dado que el producto de las 4 raíces es 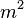 , entonces
, entonces  necesariamente.
necesariamente.


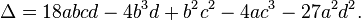




No hay comentarios:
Publicar un comentario