martes, 16 de abril de 2013

Relaciones.


Una relación es un conjunto de parejas ordenadas. Si a y b son dos conjuntos cualesquiera, r es una relación de a en b sí y sólo sí r es subconjunto de a x b. y se divide en varios tipos tales como. Relación de matriz, Relación transitiva, Relación reflexiva, Relación de pertenencia Relación simétrica.
 Una relación R_{\ }^{\ }, de los conjuntos  A_1, A_2, \ldots , A_n es un subconjunto del producto cartesiano
R\subseteq A_1 \times A_2 \times \ldots \times A_n
Una relación binaria es una relación entre dos conjuntos.
El concepto de relación implica la idea de enumeración, de algunos de los elementos, de los conjuntos que forman tuplas.
R(a_1,a_2, \ldots ,a_n) \qquad \mbox{o bien} \qquad (a_1,a_2, \ldots ,a_n) \in R
Un caso particular es cuando todos los conjuntos de la relación son iguales:  A_1 = A_2 = \ldots = A_n  en este caso se representa  A \times A \times \ldots \times A  como  A^n \, , pudiéndose decir que la relación pertenece a A a la n.
R\subseteq A^n

En las relaciones se diferencian los tipos según el número de conjuntos en el producto cartesiano, que es el número de términos de la relación:
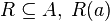
Relación unaria: un solo conjunto  R \subseteq A , \; R(a)
Relación binaria: con dos conjuntos  R \subseteq A_1 \times A_2 , \; R(a_1,a_2)
Relación ternaria: con tres conjuntos  R \subseteq A_1 \times A_2 \times A_3 , \; R(a_1,a_2,a_3)
Relación cuaternaria: con cuatro conjuntos  R \subseteq A_1 \times A_2 \times A_3 \times A_4 , \; R(a_1,a_2,a_3,a_4)
...
Relación n-aria: caso general con n conjuntos  R \subseteq A_1 \times A_2 \ldots \times A_n , \; R(a_1,a_2,\ldots,a_n)
Ejemplos:
1.- Sea R la relación “menor que” definida en el conjunto Z de los n´umeros enteros.
Escribiremos 3 < 5 para indicar que (3,5) ∈ R y 5 </ 3 para indicar que (3,5) ∈/ R

2.- Sea R la relación “es un múltiplo de” en el conjunto de los enteros positivos.
Entonces, 4R2 pero 2R/ 4. Más generalmente, xRy si, y sólo si x = ky para algún k ∈ Z
+. As´ı
para todo x, xR1. Si p > 1, entonces p es primo si xRp implica que x = 1 ´o x = p. Un n´umero x
es impar si xR/ 2.

3.- Cuando un compilador traduce un programa informático construye una tabla de símbolos que
contiene los nombres de los símbolos presentes en el programa, los atributos asociados a cada
nombre y las sentencias de programa en las que están presentes cada uno de los nombres. As´ı pues,
si S es el conjunto de los símbolos, A es el conjunto de los posibles atributos y P es el conjunto de
las sentencias de programa, entonces la tabla de símbolos incluye información representada por las
relaciones binarias de S a A y de S a P.
4.- Como dijimos anteriormente, una relación binaria sobre el conjunto de los n´umeros reales puede representarse gráficamente en el plano cartesiano. La figura siguiente es la gráfica de la relación
R = {(x, y) ∈ R × R : |x| + |y| = 1}


5.- Sea A = {1,2,3} y R = {(1,2),(1,3),(3,2)}. R es una relaci´on en A ya que es un
subconjunto de A × A. Con respecto a esta relaci´on, tendremos que
1R2, 1R3, 3R2, pero 1R/ 1, 2R/ 1, 2R/ 2, 2R/ 3, 3R/ 1, 3R/ 3

Para los conjuntos U = {1,2,3,4,5}, A = {1,2,3}, B = {2,4,5}, determinar:
6.- |A × B|.
7.- El número de relaciones de A a B.
8.- El número de relaciones binarias en A.
9.- El número de relaciones de A a B que contengan al (1,2) y al (1,5).
10.- El número de relaciones de A a B que contengan exactamente cinco pares ordenados.
11.- El número de relaciones binarias en A que contengan siete elementos como mínimo.

6.- |A × B| = |A| · |B| = 3 · 3 = 9
7.- Sea N el n´umero de relaciones de A a B.
Como una relaci´on es cualquier subconjunto del producto cartesiano de A por B, el n´umero de
relaciones de A a B será igual al n´umero de subconjuntos que tenga A × B, es decir, el n´umero de
elementos del conjunto de las partes de este conjunto, por tanto,
N = |P(A × B)| = 2|A×B| = 29
8.- Igual que en el apartado anterior, si N es el n´umero pedido, entonces
N = |P(A × A)| = 2|A×A| = 29
9.- Si eliminamos del producto cartesiano de A y B los pares (1,2) y (1,5), quedarán 7 pares, luego
el n´umero de posibles relaciones que pueden establecerse sin ellos ser´a 27
igual al n´umero N de
relaciones que contienen a los dos pares dados ya que bastaría con añadirlos a cada una de las
relaciones que no los tienen, por tanto,
N = 27

10.- Dos subconjuntos con cinco pares del producto cartesiano de A y B, serán distintos sólo si se
diferencian en algún par sin que el orden en que los mismos figuren en el subconjunto influya para
nada, por tanto, el número de subconjuntos de A×B con cinco pares ser´a igual al de combinaciones
de nueve elementos tomados cinco a cinco, es decir, si N es el n´umero pedido, entonces
N = C9,5 = (9   5) = 126
11.-  Sea Ni el n´umero de relaciones que contienen i elementos y sea N el n´umero pedido. Entonces,
N = N7 + N8 + N9
y razonando igual que en el apartado anterior,

13.-
14.- 


15.- 
    Un consumidor desea adquirir cualquier producto, este depende del precio en que el artículo esté disponible. Una relación que especifique la cantidad de un artículo determinado que los consumidores estén dispuestos a comprar, a varios niveles de precios, se denomina ley de demanda. La ley más simple es una relación del tipo P= mx + b, donde P es el precio por unidad del artículo y m y b son constantes.


16.- El cuadrado de una variable. 

17.- Diagrama sagital, representación de dos conjuntos de elementos empleando fechas. 

18.- Parejas ordenadas, describe los puntos P(x,y)

(0,0), (1,1), (2,4), (3,9).

19.- Tabla. 
 
  Describe los elementos del dominio y rango de forma vertical u horizontal. 

20.- Analítica.
 
   Modelo matemático que muestra dos variables 
    y=x^2

Publicado por en

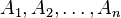
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)