FUNCIONES
Una función f de un conjunto A en un conjunto B es una regla que hace corresponder a cada elemento x perteneciente al conjunto A, uno y solo un elemento y del conjunto B, llamado imagen de x por f, que se denota y=f (x). En símbolos, se expresa f : A→ B , siendo el conjunto A el dominio de f, y el conjunto B el codominio
FUNCIONES POLINÓMICAS
Estas funciones están definidas para todos los números reales, y constituyen una de las familias de funciones que representan la mayor cantidad de fenómenos naturales. Las funciones polinómicas son aquellas cuya expresión es un polinomio, como por ejemplo:
f(x)=3x4-5x+6
Como se insinuó anteriormente, se trata de funciones continuas cuyo dominio es el conjunto de los números reales.
Pueden ser:
-Funciones Polinómicas Constantes.
-Funciones Polinómicas de Primer Grado.
-Funciones Polinómicas de Segundo Grado.Características de las funciones de grado cero.
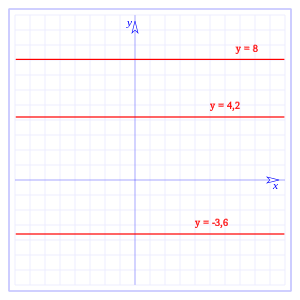
En matemática se llama función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable independiente. Se la representa de la forma:1
donde c es la constante.
Como se puede ver es una recta horizontal en el plano cartesiano, en la gráfica la hemos representado en el plano, pero, como se puede ver la función no depende de x, si hacemos:
tenemos:
donde c tiene un valor constante, en la gráfica tenemos representadas:
Como la variable dependiente y no depende de x tenemos que:
la variación de y respecto a x es cero
La integral de la función constante:
es:
![Y =
\int_a^b c\,dx
\; \rightarrow \quad
Y =
c \; \int_a^b dx
\; \rightarrow \quad
Y =
c \; x \Big ]_a^b
\; \rightarrow \quad
Y =
c \; (b-a)](https://upload.wikimedia.org/math/9/1/7/91708e506c2ee42c07764057ed9e0176.png)
- FUNCIÓN DE 1er GRADO: Son todas aquellas en las cuales los términos "x" y "y" aparecen todos elevados a potencia 1; y además sus gráficas son siempre líneas rectas en el plano cartesiano.
- FUNCIONES POLINÓMICAS DE PRIMER GRADO:Son funciones cuya gráfica es una recta, vienen expresadas por polinomios de grado uno, es decir, donde las variables están elevadas a la potencia 1.Las funciones polinómicas de primer grado son funciones del tipo f(x) = mx + n, donde m es la pendiente y n es la ordenada en el origen.En la función f(x) = mx + n se pueden presentar que:n = 0, la función se denomina función lineal o de proporcionalidad directa. Su gráfica pasa por el origen de coordenadas. Estas funciones relacionan dos variables directamente proporcionales.m y n son distintos de 0, la función se llama función afín.
Características de funciones de grado 2.
En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida como:en donde a, b y c son números reales (constantes) y a es distinto de 0.La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.Raíces.
Las raíces (o ceros) de una función cuadrática, como en toda función, son los valores de x, para los cuales. Por tratarse de un polinomio de grado 2, habrá a lo sumo 2 raíces, denotadas habitualmente como:
y
, dependiendo del valor del discriminante Δ definido como
.
- Dos soluciones reales y diferentes si el discriminante es positivo:
-
.
- Una solución real doble si el discriminante es cero:
- Dos números complejos conjugados si el discriminante es negativo:
Características de funciones polinomiales de grado uno.
En geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:
donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica m entonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.
Algunos autores llaman función lineal a aquella con b= 0 de la forma:
mientras que llaman función afín a la que tiene la forma:
cuando b es distinto de cero.
Una función lineal de una única variable dependiente x es de la forma:
que se conoce como ecuación de la recta en el plano x,y.
En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:
en esta recta el parámetro m= 1/2 por tanto de pendiente 1/2, es decir, cuando aumentamos x en una unidad entonces y aumenta en 1/2 unidad, el valor de b es 2, luego la recta corta el eje y en el punto y= 2.
En la ecuación:
la pendiente de la recta es el parámetro m= -1, es decir, cuando el valor de x aumenta en una unidad, el valor de y disminuye en una unidad; el corte con el eje y es en y= 5, dado que el valor de b= 5.
En una recta el valor de m se corresponde al ángulo  de inclinación de la recta con el eje de las x a través de la expresión:
de inclinación de la recta con el eje de las x a través de la expresión:
Las funciones de segundo grado o parabólicas tienen mucho uso dentro del mundo de los videojuegos, piensa en Super Mario o en cualquier juego de plataformas 2D que hayas jugado. Cuando saltas el movimiento que describe el personaje es un movimiento parabólico que se puede obtener con una función de segundo grado. Tienen el siguiente aspecto.
Donde a, b y c son números. Si a vale 0 nos quedaría.
Que ya no sería una parábola sino una recta como vimos en el artículo anterior. La gráfica de la parábola es la siguiente.
Esta sería la parábola más básica, la del tipo:
Para dibujar su gráfica podríamos usar el método de ir dándole valores a la x y obtener sus respectivas y, pero necesitaríamos muchos puntos para poder dibujar bien, lo mejor es buscar los puntos claves. Los puntos de corte con los ejes y el vértice.
Veamos un ejemplo, representar la siguiente parábola:
Para saber en que punto corta al eje y debemos darle a la x el valor 0, así sabremos cuanto vale la y en el eje.
Bien ya tenemos un punto de nuestra parábola.

Ahora calculemos los puntos de corte con el eje x, esto lo hacemos dando a la y el valor 0. Nos daría la siguiente ecuación.
Que es una ecuación de segundo grado que se resuelve con la siguiente fórmula.
Sustituimos valores y obtenemos dos puntos (recuerda que una raiz devuelve dos valores uno con signo más y otro con signo menos).
Por último calculamos el vértice de la parábola que viene dado por la siguiente fórmula.
Este es el valor de la x del vértice, para hallar su y simplemente sustituimos el valor en la función.
Resolvemos y tenemos que el vértice es el punto.
Ahora solo nos queda marcar los puntos en el eje de coordenadas y obtener la gráfica.
Te recomiendo que veas el video que está en el siguiente enlace:


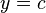



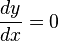
feo
ResponderEliminar