En matemática se llama función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable independiente. Se la representa de la forma:1
donde c es la constante.
Como se puede ver es una recta horizontal en el plano cartesiano, en la gráfica la hemos representado en el plano, pero, como se puede ver la función no depende de x, si hacemos:
tenemos:
donde c tiene un valor constante, en la gráfica tenemos representadas:
Como la variable dependiente y no depende de x tenemos que:
la variación de y respecto a x es cero
La integral de la función constante:
es:
![Y =
\int_a^b c\,dx
\; \rightarrow \quad
Y =
c \; \int_a^b dx
\; \rightarrow \quad
Y =
c \; x \Big ]_a^b
\; \rightarrow \quad
Y =
c \; (b-a)](https://upload.wikimedia.org/math/9/1/7/91708e506c2ee42c07764057ed9e0176.png)
- La función constante es del tipo:y = nEl criterio viene dado por un número real.La pendiente es 0.La gráfica es una recta horizontal paralela a al eje de abscisas.
Rectas verticales
Las rectas paralelas al eje de ordenadas no son funciones, ya que un valor de x tiene infinitas imágenes y para que sea función sólo puede tener una. Son del tipo:x = KEjemplos:Para los ejemplos siguientes sólo serán pocos, puesto que el tema es
demasiado fácil de comprender. ;DAquí te dejo unos vídeos muy fáciles, ...


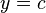



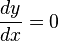
No hay comentarios:
Publicar un comentario